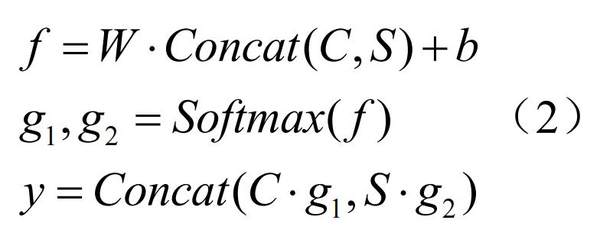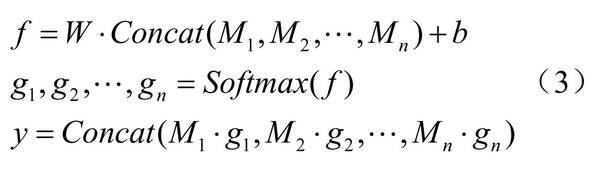李冠霖

　　摘要：随着时间序列分析技术的飞速发展，多元时间序列分类技术已广泛应用于故障检测、电气工程、模式识别等多个领域。本研究提出一种新型的多元时间序列分类方法，并在复杂的场景下进行应用与验证。基于多模态信号数据，考虑了数据的时间依赖性与空间依赖性，构建了一种专为多元时间序列信号设计的深度学习框架。特征提取模块通过应用注意力机制获取时间和空间特征，构建了适应性强的特征空间。多模态信号融合部分，研究采用门控融合多元数据特征，显著地提高了分类准确率。通过准确率、召回率和F1分数等多角度评估标准，验证了模型的泛化能力。数值实验证实了分类框架在多元时间序列信号处理的有效性，并为模型的优化提供了新的视角。研究将探索模型在更广泛数据集上的可扩展性，加强模型的实时分类能力，并期待算法在交叉领域中的新应用。

　　关键词：多元时间序列分类；模式识别；深度学习；特征提取
 

　　1. 引言

　　随着信息技术的飞速发展，多模态信号在各个领域中的应用日益广泛，如生物医学^[1]、电气工程^[2]、故障检测^[2]等。这些信号通常包含多种类型的时间序列数据，它们在时间维度上呈现出复杂且非线性的特征。多元时间序列分析作为一种处理多模态信号的有效方法，能够综合分析不同模态之间的关联性，从而提高信号识别的准确性和效率。

　　尽管已有众多研究对多元时间序列分类算法进行了改进，但在多模态信号识别方面，仍面临许多挑战^[3]。当前的研究大多集中在算法优化上，而对多模态信号的时空特征的提取与融合相对薄弱。此外，由于多元时间序列数据量大、特性复杂，往往需要结合多种方法才能获得准确的结果，这使得现有研究的应用范围受到限制。

　　为了解决这些问题，研究者们开始引入人工智能技术，尤其是机器学习和深度学习方法，以提高多元时间序列数据的分类精度^{[4, 5]}。这些方法能够有效挖掘数据中的时序特征，并为信号的模式识别提供有力支持。通过对提取出的特征进行相应处理，研究者们希望能够实现对多元时间序列的准确分类，从而提升系统的可靠性和安全性。

　　本文以多模态信号为研究对象，对多元时间序列分类算法进行研究。多元时间序列数据具有复杂性和动态性，数据的多样性和瞬时性对系统的性能分析和模式识别提出了更高的要求。本研究的主要目的是提出一个新的基于深度学习的多元时间序列分类方法，为多模态信号识别提供理论支持和实际指导，从而提高相关系统的智能化水平。

　　本研究的主要贡献如下：

　　首先，系统梳理了多元时间序列的基本概念，并介绍了多元时间序列分类中常用的算法和模型，包括机器学习、深度学习等技术。其次，提出了一种基于深度学习的结合门控的多元时间序列分类方法。再次，针对多模态信号进行数值实验及可视化分析，说明了模型的有效性。最后，提出了未来的研究方向和改进建议，旨在为多模态信号的自动化识别提供参考。

　　2.相关工作

　　时间序列分类技术是一项用于识别时序数据模式的重要方法，在电气工程^[6]、医疗保健^[7]、交通^[4]等领域应用广泛。时间序列数据集通常由实时传感器生成，每个样本包括一个（单变量时间序列)或多个（多变量时间序列）维度。因此，按照时间序列的维数可以分为单变量时间序列分类方法^[8]和多元时间序列分类^[9]方法。

　　多变量时间序列具有复杂的相互依赖关系，包括单变量的时序特征以及不同变量间的关系特征，因此，多变量时间序列分类比单变量时间序列分类更具挑战性。

　　为了解决多元时间序列分类问题，学者们提出了许多研究方法，主要包括传统的时序分析方法和基于深度学习的方法。

　　传统的时序分析方法应用最广泛的是动态时间规整(Dynamic Time Warping, DTW)算法^[10]，该算法用于测量两个序列之间的相似性，这些序列在时间或空间上可能有所不同。相似性的衡量是通过计算两个时间序列之间的距离来实现的，相近的样本更有可能被分配到相同的标签。 随后，一些学者^[11]对此方法进行改进，提出了一些基于动态时间规整算法的变种。ShapeNet^[12]也是一种经典且有影响力的基于形状的多元时间序列分类方法。随后，一些学者^{[13, 14]}对此方法进行改进。

　　近年来，随着人工智能的发展，基于深度学习的方法越来越受到研究人员的关注，并逐渐成为时间序列数据分析领域的主流方法^[15]。

　　卷积神经网络(CNNs)因其捕获局部特征的有效性而被广泛应用于时间序列分类任务中。比如，文献^[16]初步探索了基于卷积神经网络的多元时间序列分析方法并将其用于动作识别，文献^[17]提出了MCNN模型，该模型设计了一个多分支卷积神经网络层用于捕获时间序列特征。

　　循环神经网络(RNNs)^[18]也被广泛用于捕获时间序列数据中存在的长期和短期时间依赖性。文献^[19]设计了MF-Net模型，该模型集成了全局-局部模块和稀疏自注意力机制，分别用来获取局部和全局特征。此外，该模型还结合了一个空间局部块来捕获多元时间序列数据中存在的空间依赖性。文献^[20]提出了一种TCRAN模型，该模型集成了时间残差通道注意模块、自适应通道特征调整机制和双向门控循环单元，能够提取时间序列中的长期时间依赖性，提高分类性能。

　　图神经网络(GNNs)是一类专门用于处理图结构数据的深度学习方法。它们的出现为多元时间序列数据分析提供了新的方法。GNNs在捕获多元时间序列固有的空间依赖性方面表现出卓越的能力，因此被广泛应用于各种任务，如多元时间序列预测^[21]、异常检测^[22]、分类^[23]。TodyNet^[24]是基于深度图的代表性方法，它引入了动态图机制来提取多元时间序列内部的时空依赖关系和不同时间段的相互关系。文献^[25]针对多元时间序列分类任务构建了一个时频域特征融合网络(TF-Net)，该模型包含两个模块：时域模块以及频域模块。时域模块由CNNs和图卷积神经网络(GCNs)组成，用于捕获的时域特征;频域模块用于捕获多元时间序列数据的频域特征。

　　Transformer网络作为新型的深度学习方法最初是为了解决机器翻译任务而设计的^[26]。随后，Transformer网络被应用于自然语言处理、图像处理^{[27, 28]}等领域。Transformer网络的核心是自注意力机制，它可以保持输入元素集合的顺序和趋势。因此，该方法非常适用于学习时间序列特征。越来越多的文献开始采用Transformer网络来学习时间特征，近年来取得了显著的成果。例如，文献^{[29, 30]}将Transformer应用于预测和回归任务。文献^[30]探讨了Transformer在临床时间序列数据分类中的应用。最新的工作是文献^[5]，作者研究了Transformer在多元时间序列分类中的应用。尽管Transformer在许多领域得到了广泛应用，但在时间序列分类上应用Transformer网络的算法相对较少。本研究基于深度学习对时间序列分类方法进行研究，构建了一个结合门控的Transformer网络用于多模态的信号识别。

　　3.多元时间序列基础

　　多元时间序列是指在同一时间间隔内收集的两个或多个相关变量的数据集。与单变量时间序列相比，多元时间序列考虑了多个变量之间的相互关系，这使得其在分析动态系统中的变化更具价值。

　　4.网络结构

　　本文的Transformer网络设计建立在多个领域和任务改进的基础上，文献^[5]研究了对当前Transformer网络进行简单扩展的带门控结构，命名为门控Transformer网络(GTN)，用于多元时间序列分类问题。在他们研究的基础上，本文针对多元信号数据采用多个门控Transformer网络，并用门控融合多模态信号的特征。本文模型架构如图1所示。本研究模型的总体架构包括带门控的时空特征提取模块，门控融合模块以及分类解码器。

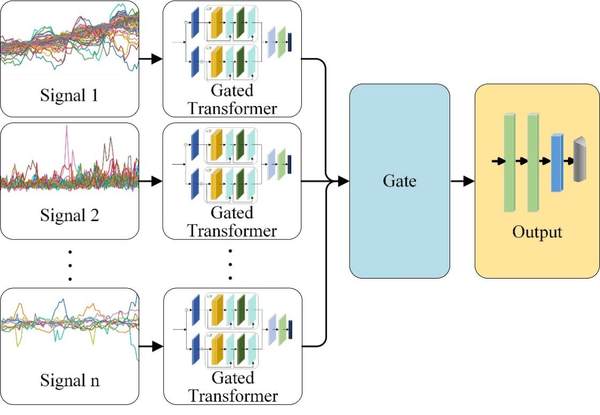
　　图1 网络结构图

　　4.1门控Transformer网络

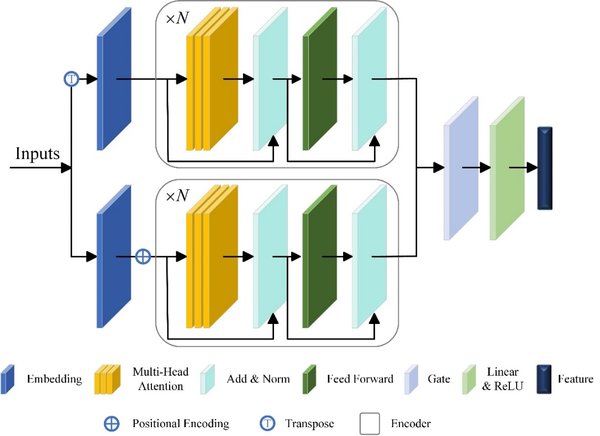
　　图2门控Transformer网络

　　本文采用的门控Transformer网络^[5]模块如图2所示，包括时间模块、空间模块、门控层。

　　时间模块包括输入嵌入模块、位置编码、堆叠的编码器。在时间特征提取模块中，用位置编码模块来区分序列的时间先后。每个编码器包含多头自注意力机制和一个全连接的前馈网络。在多头注意力和前馈网络之后，紧接着归一化。经过时间模块后，可以获得时间模块输出特征，它是后续门控的一个输入。

　　空间模块的作用是发现不同距离通道之间的依赖关系。通过转置通道和时间轴来获得该编码器的输入，结构类似于时间模块，因为通道之间没有明确的位置关系，因此，空间模块没有使用位置编码。空间模块的特征输出也作为后续门控的一个输入。

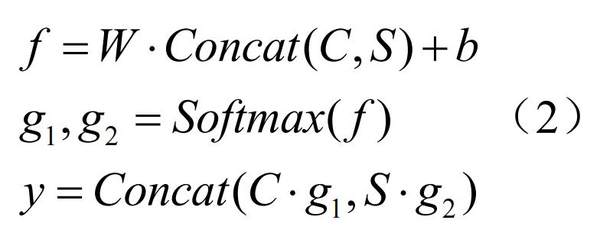
　　4.2门控融合模块和分类解码器

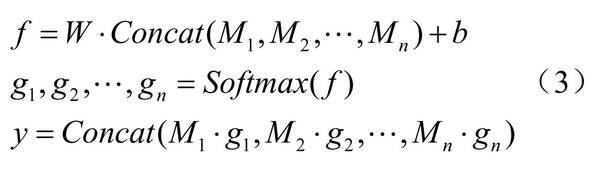
　　分类解码器如图1所示，将经过门控融合后的特征输入到分类解码器中，该解码器由三个级联的前馈神经网络组成：两个LR(结合线性层和ReLU层)和一个LS(结合线性层和Softmax层)，以预测最终的分类分数。分数最高的类别被分配为类别标签。

　　5.模型效果评估

　　在多元时间序列分类问题的研究中，模型效果评估可以保证算法的可靠性与有效性。评估标准通常包括准确率(Accuracy)、召回率(Recall)、F1分数(F1-score)等，能够全面反映模型的性能。本文采用交叉验证技术，常见的k折交叉验证能够有效避免过拟合，确保评估结果的稳健性。本文在PD-Walk^[31]数据集上进行实验，数据集涉及正常和异常两种模式的步态信号，首先通过计算数据集的多个模态信息包括距离，速度，加速度等，获取了多模态的时间序列数据，五折交叉验证结果如表1所示，本文模型获得了85.8%的准确率、86.8%的召回率和86.0%的F1分数。

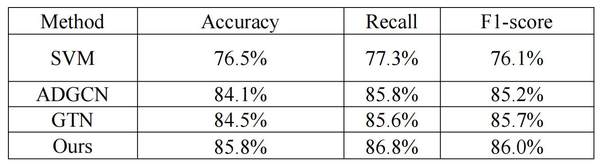
　　从表2可以看出，本文模型在性能上优于其他方法。SVM作为基准达到了76.5%的准确率。参考文献^[31]提出了ADGCN，它能够达到84.1%的准确率。相比之下，GTN[5]方法达到了84.5%的准确率。本文模型以85.8%的准确率、86.8%的召回率和86.0%的F1分数超过了它们。

　　表1. 五折交叉验证

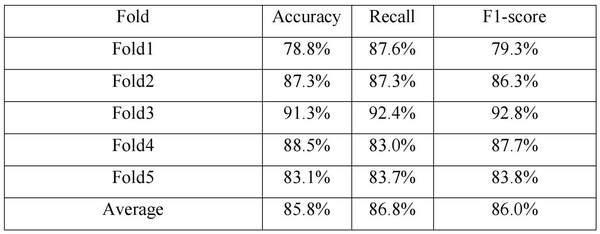
　　表2. 准确率、召回率和F1分数方面的总体表现

　　6.结论

　　本研究采用多元时间序列分类方法对多模态信号进行了系统分析与处理，构建了注意力机制与门控相结合的深度学习模型，对数据进行了特征提取与分类。数据集涉及正常和异常两种模式，通过使用交叉验证方法，模型在多元时间序列分类的平均准确率达到了85.8%，确保了模型的泛化能力，表明多元时间序列分类在多元信号模式识别中的应用前景良好。通过与其他算法的性能比较，表明本文模型在准确率、召回率和F1分数方面的优越性。此外，本研究在解释性方面也进行了尝试，结合注意图对时间序列进行了分析，增进了对模型判断依据的理解，同时为后续的实际应用提供理论支撑。

　　未来研究方向主要集中在提高多元时间序列分类的准确性与效率上。采用深度学习模型与传统方法的结合，将有助于捕捉时间序列中的复杂模式。研究可围绕不同类型数据的特征提取方法展开，如使用小波变换进行多尺度分析，以更好地处理非平稳信号。针对多元时间序列的时序相关性，后续可以利用图神经网络将帮助构建复杂的系统网络结构，从而提升分类效果。此外，考虑到数据量的庞大与实时处理需求，轻量级模型的研究将成为重点，未来可进一步探索其在实际应用中的潜力与价值。

　　参考文献

　　[1] Daliri M R. Chi-square distance kernel of the gaits for the diagnosis of Parkinson's disease [J]. Biomedical Signal Processing and Control, 2013, 8(1): 66-70.

　　[2] 唐文虎, 牛哲文, 赵柏宁, et al. 数据驱动的人工智能技术在电力设备状态分析中的研究与应用 [J]. 高电压技术, 2020, 46(9): 2985-2999.

　　[3] 文成林, 吕菲亚, 包哲静, et al. 基于数据驱动的微小故障诊断方法综述 [J]. 自动化学报, 2016, 42(9): 1285-1299.

　　[4] Qin D, Peng Z, Wu L. Deep attention fuzzy cognitive maps for interpretable multivariate time series prediction [J]. Knowledge-Based Systems, 2023, 275110700.

　　[5] Liu M, Ren S, Ma S, et al. Gated transformer networks for multivariate time series classification [J]. arXiv preprint arXiv:210314438, 2021.

　　[6] 任巍曦, 张文煜, 李明, et al. 基于数字孪生的风电机组轴承故障诊断方法研究 [J]. 弹箭与制导学报, 2022, 42(3): 97-104.

　　[7] Kang H, Choi S. Bayesian common spatial patterns for multi-subject EEG classification [J]. Neural Networks, 2014, 5739-50.

　　[8] Del Campo F A, Neri M C G, Villegas O O V, et al. Auto-adaptive multilayer perceptron for univariate time series classification [J]. Expert Systems with Applications, 2021, 181115147.

　　[9] Yang C, Wang X, Yao L, et al. Dyformer: A dynamic transformer-based architecture for multivariate time series classification [J]. Information Sciences, 2024, 656119881.

　　[10] Keogh E, Ratanamahatana C A. Exact indexing of dynamic time warping [J]. Knowledge and information systems, 2005, 7358-386.

　　[11] Shokoohi-Yekta M, Wang J, Keogh E. On the non-trivial generalization of dynamic time warping to the multi-dimensional case; proceedings of the Proceedings of the 2015 SIAM international conference on data mining, F, 2015 [C]. SIAM.

　　[12] Ye L, Keogh E. Time series shapelets: a novel technique that allows accurate, interpretable and fast classification [J]. Data mining and knowledge discovery, 2011, 22149-182.

　　[13] Karlsson I, Papapetrou P, Boström H. Generalized random shapelet forests [J]. Data mining and knowledge discovery, 2016, 301053-1085.

　　[14] Bostrom A, Bagnall A. A shapelet transform for multivariate time series classification [J]. arXiv preprint arXiv:171206428, 2017.

　　[15] Zhang Y, Hou Y, Ouyang K, et al. Multi-scale signed recurrence plot based time series classification using inception architectural networks [J]. Pattern Recognition, 2022, 123108385.

　　[16] Yang J, Nguyen M N, San P P, et al. Deep convolutional neural networks on multichannel time series for human activity recognition; proceedings of the Ijcai, F, 2015 [C]. Buenos Aires, Argentina.

　　[17] Cui Z, Chen W, Chen Y. Multi-scale convolutional neural networks for time series classification [J]. arXiv preprint arXiv:160306995, 2016.

　　[18] Hao S, Wang Z, Alexander A D, et al. MICOS: Mixed supervised contrastive learning for multivariate time series classification [J]. Knowledge-Based Systems, 2023, 260110158.

　　[19] Du M, Wei Y, Zheng X, et al. Multi-feature based network for multivariate time series classification [J]. Information Sciences, 2023, 639119009.

　　[20] Zhu H, Zhang J, Cui H, et al. TCRAN: Multivariate time series classification using residual channel attention networks with time correction [J]. Applied Soft Computing, 2022, 114108117.

　　[21] Chen Y, Ding F, Zhai L. Multi-scale temporal features extraction based graph convolutional network with attention for multivariate time series prediction [J]. Expert Systems with Applications, 2022, 200117011.

　　[22] Shi Y, Wang B, Yu Y, et al. Robust anomaly detection for multivariate time series through temporal GCNs and attention-based VAE [J]. Knowledge-Based Systems, 2023, 275110725.

　　[23] Duan Z, Xu H, Wang Y, et al. Multivariate time-series classification with hierarchical variational graph pooling [J]. Neural Networks, 2022, 154481-490.

　　[24] Liu H, Yang D, Liu X, et al. Todynet: temporal dynamic graph neural network for multivariate time series classification [J]. Information Sciences, 2024, 677120914.

　　[25] Lei T, Li J, Yang K. Time and frequency-domain feature fusion network for multivariate time series classification [J]. Expert Systems with Applications, 2024, 252124155.

　　[26] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need [J]. Advances in neural information processing systems, 2017, 30.

　　[27] Yang Z, Dai Z, Yang Y, et al. Xlnet: Generalized autoregressive pretraining for language understanding [J]. Advances in neural information processing systems, 2019, 32.

　　[28] Zhao H, Jia J, Koltun V. Exploring self-attention for image recognition; proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, F, 2020 [C].

　　[29] Li S, Jin X, Xuan Y, et al. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting [J]. Advances in neural information processing systems, 2019, 32.

　　[30] Oh J, Wang J, Wiens J. Learning to exploit invariances in clinical time-series data using sequence transformer networks; proceedings of the Machine learning for healthcare conference, F, 2018 [C]. PMLR.

　　[31] He Y, Yang T, Yang C, et al. Integrated Equipment for Parkinson's Disease Early Detection Using Graph Convolution Network [J]. Electronics, 2022, 11(7): 1154.

　　（作者单位河南科技大学，数学与统计学院，数学与应用数学专业)